红黑树
红黑树的定义
- 在算法导论中:
- Every node is either red or black.
- The root is black.
- Every leaf is black.(the last node)
- if a node is red,then both its children are black.
- For each node,all simple paths from the node to descendant leaves contain the same number of black nodes.
- 如果直接看上面的定义,我们可能一开始就会懵逼.接下来我们将从2-3树开始讲起.
红黑树与2-3树的等价性
我们先从2-3树开始说起
2-3树
- 满足二分搜索树的基本性质
- 但是其并不是二叉树,它的节点可以存放一个元素或者两个元素
- 存放两个元素的那个节点有三个孩子.
- 我们将存放一个元素有两个孩子的叫做2节点,存放两个元素有三个孩子的叫做3节点
- 2-3树是一棵绝对平衡的树.(即任意节点的左右子树的高度是相等的)
2-3树是如何维持绝对的平衡
当从一个空树中添加元素时,和二分搜索树一样,成为其根节点.
再往其中添加元素,要始终记得一点,2-3树添加元素时一定不会往空节点中添加,当他碰到根节点时,会自动合并
成为一个3节点.
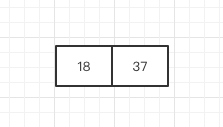
当在往其中添加一个元素时,同样遵循上面的规则,此时会变成一个4节点.
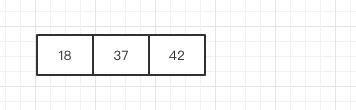
但是2-3树中只应该有2节点或者3节点,此时2-3树会自动变形
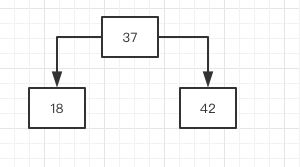
从而变成一棵平衡二叉树.
我们再往里面添加元素.
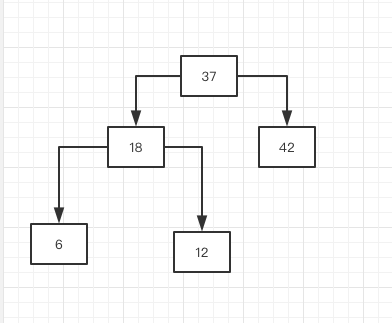
很显然此时并不是一棵平衡的树,那么2-3树又会进行一次变形
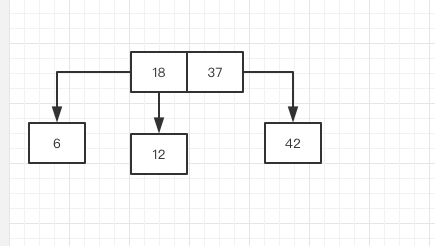
这就是2-3树的逻辑!这样的话,在添加元素后,2-3树始终是一棵绝对平衡的树.
2-3树在添加元素时,不会向二分搜索树那样,添加到一个空的节点的位置,一定是添加到最后搜索到的那个叶子节点与其进行融合.
为什么说红黑树和2-3树等价?
在前面我们详细介绍了2-3树,2-3树中2节点和3节点,其中2节点中只存在一个元素,3节点中存在两个元素.
在红黑树中,我们用两个连着的节点来表示3节点.
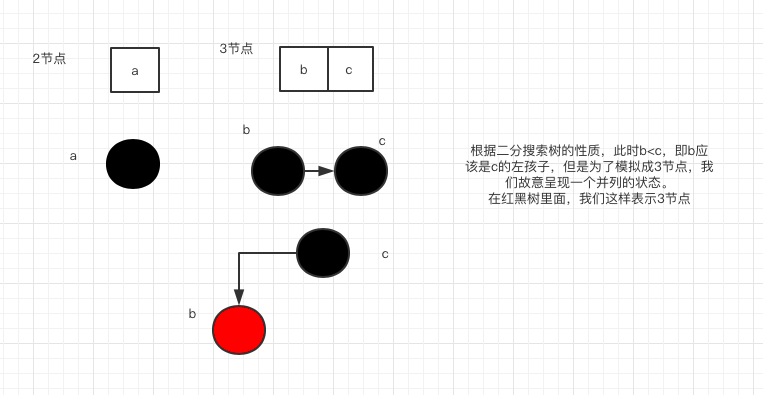
即红黑树中所有的红色节点都是左倾斜的.
接下来我们举个例子,然后再回过头来看一下最开始的那五句话.
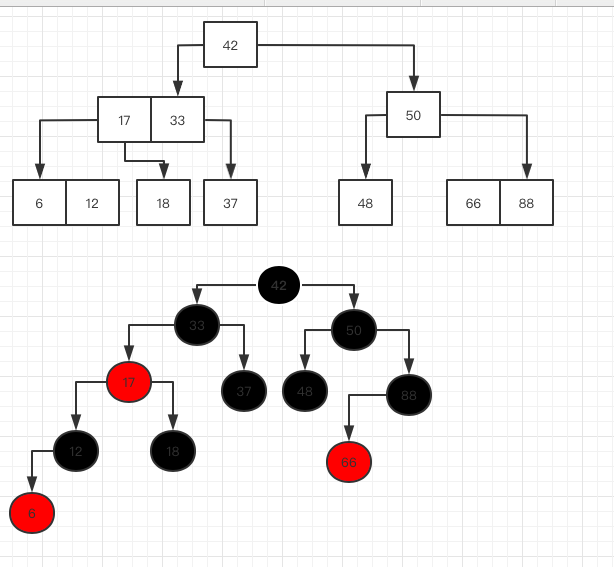
如果真正明白了2-3树和红黑树之间的关系,那么上面的图应该不难.
- 每个节点要么是红色的,要么是黑色的.
- 根节点是黑色的.
- 每一个叶子节点(最后的空节点)是黑色的.
- 如果一个节点是红色的,那么他的孩子节点都是黑色的.
- 从任意一个节点到叶子节点,经过的黑色节点是一样的.
1、第一条性质我们可以很明显的看出来.
2、由于在2-3树中,根节点要么是2节点或者3节点,不管是2节点还是3节点,在红黑树表示中,都是黑色节点.
3、这里的叶子节点是指空节点,而不是我们以前所认识到的左右子树都为空的节点.即一棵空树也是红黑树,这里就与第二条性质所对应起来了,即根节点-空节点都是黑色的.
4、在红黑树中,只有一种情况会出现红色节点,即他原来表示的是一个3节点时,3节点对应的左侧的节点在红黑树中表示为红色节点。不管他的左孩子还是右孩子,连接的都是一个2节点。即左右孩子都是黑色的。就算他连接一个三节点,我们也是先连接黑色节点,再连接红色节点,这样看来,第4条性质也很好理解了。
5、2-3树是一棵绝对平衡的树,即从任意节点出发,到叶子节点,所经过的节点数是相等的。在2-3树中,不管是2节点还是3节点,都会有一个黑色节点。即我们从红黑树中任意一个节点出发,我们每经过一个黑色节点,就像是以前在2-3树经过了一个节点。区别仅仅是,如果红黑树的左孩子为红色的话,就相当于我们以前经过了一个3节点,如果左孩子是黑色的话,相当于我们之前经过的是一个2节点。那么这样我们再来理解第五句话,即从任意一个节点到叶子节点,经过的黑色节点是一样的,就非常好理解了。

