AVL

2020-04-17

AVL树

AVL树是最早的自平衡二分搜索树结构

在之前我们详细设计了一棵二分搜索树。但是我们想象这样一种情况，如果我们在添加元素时，只是往一个方向添加元素，二分搜索树的特性就是左孩子的所有节点的值一定比该节点的值少，如果我们总是添加比这个节点值小的元素，那么我们将一直往左边添加，此时二分搜索树会退化成一条链表。而链表的很多操作的时间复杂度都为O(n)，而二分搜索树则为O(logn)。那么我们此时该如何将这种”链表”重新转换为一棵”树“呢？

AVL树的概念

所谓AVL树，就是任意节点左右孩子的高度差不超过1.

通过上述的概述，我们很容易的就是想到，我们可以给树重新定义一个属性，即他的高度.

private class Node{
       public E e;
       public Node left;
       public Node right;
       public int height;
       public Node(E e){
           this.e=e;
           left=null;
           right=null;
          height=1;
       }
  
   }

为了方便，我们再定义一个方法

// 获得节点node的高度
   private int getHeight(Node node){
       if(node == null)
           return 0;
       return node.height;
   }

此时，我们引入一个新的概念，为了计算左右两颗子树的高度差，我们定义平衡因子这样一个概念。

平衡因子：我们默认是左子树的高度-右子树的高度

// 获得节点node的平衡因子(左子树和右子树的高度差)
   private int getBalanceFactor(Node node){
       if(node == null)
           return 0;
       return getHeight(node.left) - getHeight(node.right);
   }

接下来以添加元素为例，看是如何进行二叉树的平衡。

如果我们一直往左边添加元素，即出现左边树比右边树高的情况

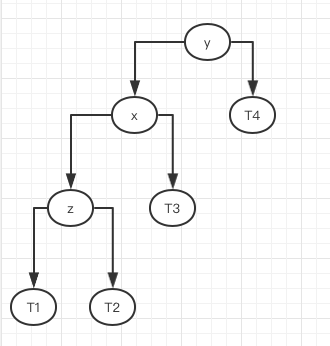
右旋转LL

此时，我们需要将这y这个节点进行右旋转

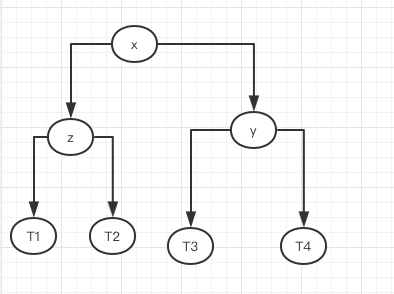
右旋转-finish

如果变成这样子，我们就可以实现将不平衡的二叉树变得平衡。

如果此时要验证该树是否是平衡的，也很简单。我们可以把每一个节点的高度值给标出来。
由于此时不平衡是由y导致的，即这种情况下以z和x为根的二叉树都是平衡二叉树。即z的左右子树高度差不会超过1，我们将二者中较大高度设为h，即此时z的高度为h+1。
x也是保持平衡的，且x的平衡因子最大为1，（参照LL的条件），参照下图，此时T3的高度要么为h+1，要么为h，x的高度值为h+2。
现在来看y这个节点，由于y打破了平衡，即它的左右子树的高差度是大于1的，但这里，至多为2.因为我们只增加了一个元素。在这种情况下，左子树比右子树的高度大了，即此时T4的高度为h。
当我们计算完所有节点的高度后，我们再来看右侧这棵树，就很容易的发现它已经实现平衡了！
当然，这种右旋转的操作也十分简单

//将不平衡的y节点右旋转
   // 对节点y进行向右旋转操作，返回旋转后新的根节点x
   //        y                              x
   //       / \                           /   \
   //      x   T4     向右旋转 (y)        z     y
   //     / \       - - - - - - - ->    / \   / \
   //    z   T3                       T1  T2 T3 T4
   //   / \
   // T1   T2
   private Node rightRotate(Node y){
       Node x=y.left;
       //将T3存起来
       Node T3=x.right;
       x.right=y;
       y.left=T3;
         //更新height   由于T1,T2,T3,T4都没有变化，
       //我们只需要更新x和y的高度值就可以了
       y.height=Math.max(getHeight(y.left),getHeight(y.right))+1;
       //先更新y的，再更新x的高度值
       x.height=Math.max(getHeight(x.right),getHeight(x.left))+1;
       return x;

   }

与此同时，在旋转过后我们要更新一下高度，并且只需要更新x节点和y节点的即可。

有了右旋转，那么就有左旋转的操作。如果右边子树比左边子树要高，即出现这种情况。

左旋转

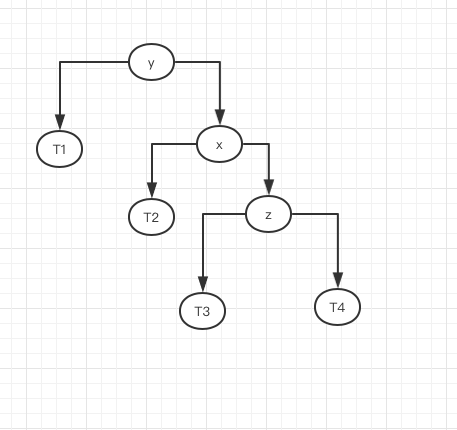
当出现这种情况时，我们需要进行左旋转操作

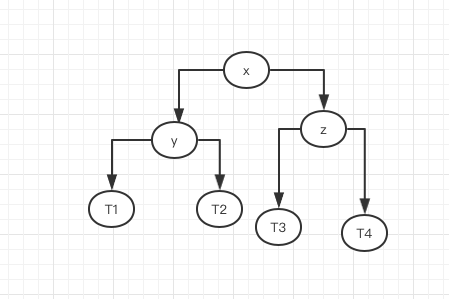
左旋转-finish

// 对节点y进行向左旋转操作，返回旋转后新的根节点x
   //    y                             x
   //  /  \                          /   \
   // T1   x      向左旋转 (y)       y     z
   //     / \   - - - - - - - ->   / \   / \
   //   T2  z                     T1 T2 T3 T4
   //      / \
   //     T3 T4
   private Node leftRotate(Node y){
       Node x=y.right;
       Node T2 =x.left;
       x.left=y;
       y.right=T2;

       //更新heigth
       //与上述右旋转一样
       y.height=Math.max(getHeight(y.left),getHeight(y.right))+1;
       //先更新y的，再更新x的高度值
       x.height=Math.max(getHeight(x.right),getHeight(x.left))+1;
       return x;
   }

有了上述操作，在引入平衡因子的情况下，我们在什么时候需要进行左旋转，什么时候进行右旋转呢？

public void add(E e){
       add(root,e);

   }

   /**
    * recursion
    * @param node
    * @param e
    * @return the root of the tree
    */
   private Node add(Node node,E e){
       if(node==null) {
           size++;
           return new Node(e);

       }
       // the number is small than  the node.val
       if(e.compareTo(node.e)<0)
           node.left=add(node.left,e);

       //the number is big than the node.val
       if(e.compareTo(node.e)>0)
           node.right=add(node.right,e);

       return node;

   }

我们先将之前的插入元素引进来.如果此时平衡因子大于1，即此时左子树的高度比右子树的高度要高，并且此时该节点的左孩子的平衡因子也要大于0，即我们需要进行右旋转操作。

//LL
       if(balanceFactor>1&&getBalanceFactor(node.left)>=0){
           //左边比右边高 ，即是向左边插入元素导致不平衡
           //右旋转
           return rightRotate(node);
       }

同样的，我们也有这样一种情况

//RR
        if(balanceFactor<-1&&getBalanceFactor(node.right)<=0){
           //右边比左边高，即是向右边插入元素导致不平衡
           //左旋转
           return   leftRotate(node);

       }

上述两种情况是最简单的情况，但并不是最一般的情况。他们分别代表了一直往左孩子中添加元素或者一直往右孩子中添加元素。我们将上述两种情况称为LL和RR。

那么接下来介绍一下LR与RL

LR：

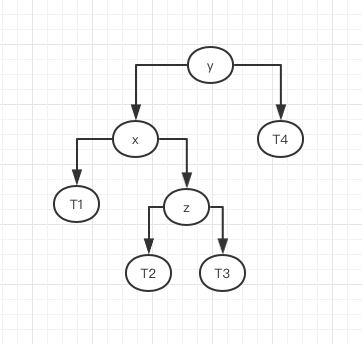
这种情况就是我们先沿着左边添加元素，然后沿着右边添加元素。此时我们如果只是进行简单的左右旋转将不能使其平衡。
此时我们先将x进行左旋转，转换为LL的情况.

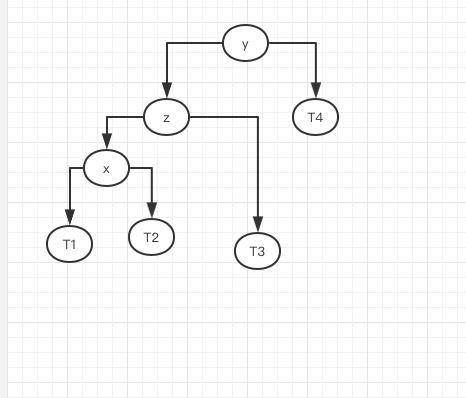
这时候就是我们熟悉的LL了，我们只需要再进行一次右旋转操作即可

//LR
       if(balanceFactor>1&&getBalanceFactor(node.left)<0){
           //左子树比右子树高
           //此时node节点的左孩子是向右倾斜的
          node.left= leftRotate(node.left);
          //此时已经转化为了LL的情况
          return rightRotate(node);
       }

相应的，我们有RL的情况，与之对应的

//RL
        if(balanceFactor<-1&&getBalanceFactor(node.right)>0){
            //此时右子树比左子树高
            //并且此时node节点的右孩子是向左倾斜的
           node.right= rightRotate(node.right);
           //此时已经转化成了RR的情况
            return leftRotate(node);
        }

这样，我们就实现了在添加操作中，如何将一棵不平衡的二叉树转换为一棵平衡的二叉树，即AVL树。