八皇后问题二

八皇后问题二

• 参照前文，我们提供了一种解八皇后问题的方法。
  • 我们采用了一个数组来记录皇后摆放的位置，即数组的索引表示皇后的行数，数组的元素值表示皇后的列数。但是仔细一想，其实我们是有一点多余的，因为我们总是要摆放完八行，即我们并不用记录行数。此时我们提供一种全新的思路。
  • 我们采用一个boolean类型的数组来记录该列有没有皇后，true表示该列有皇后，false表示该列没有皇后。
  • 对应的，我们引入另外两个boolean类型的数组，分别代表从左上角到右下角的对角线，和从右上角到左下角的对角线。
• 大致的思路还是没有变化，我们采用递归+回溯的方法进行摆放。
• 首先明确一点，当为nn的格子时，从左上角到右下角的对角线应该为2n-1条，同理，右上角到左下角的对角线应该为2n-1条，这是一个很简单的数学问题.可以验证一下

public class Main2 {
	
	
	public static void main(String[] args) {
		
		new Main2().placeQueens(8);
		
	}
	
	
	/**
	标记着某一列是否有皇后
	 */
	boolean cols[];
	/**
	 * 左上角到右下角的斜线是否有皇后
	 */
	
	boolean leftTop[];
	/**
	 * 右上角到左下角的斜线是否有皇后
	 */
	
	boolean rightTop[];
	int count;
	/**
	 * 摆放n个皇后
	 * @param n
	 */
	 void placeQueens(int n) {
		if(n<1) return;
		 cols=new boolean[n];
		 leftTop=new boolean[2*n-1];
		 rightTop=new boolean[2*n-1];
		place(0);
	
		System.out.println(n+"皇后一共有"+count+"种摆法");
		
	}
	
	
	/**
	 * 从第row行开始摆放皇后
	 * @param row
	 */
	 void place(int row) {
		 if(row==cols.length) {
			 count++;
			
			 return;
		 }
		 
		 /**
		  * 左上角->右下角的对角线索引 row-col+n-1
		  * 右上角->左下角的对角线索引 row+col
		  */
		 for(int col=0;col<cols.length;col++) {
			if(cols[col])  continue;
			int ltIndex=row-col+cols.length-1;
			if(leftTop[ltIndex]) continue;
			int rtIndex=row+col;
			if(rightTop[rtIndex]) continue;
			cols[col]=true;
			leftTop[ltIndex]=true;
			rightTop[rtIndex]=true;
			place(row+1);	 
		 }	
	}
	}

在这里简单解释一下关于对角线判定的方法

• 我们将这些对角线按照索引排列起来，如下图所示.

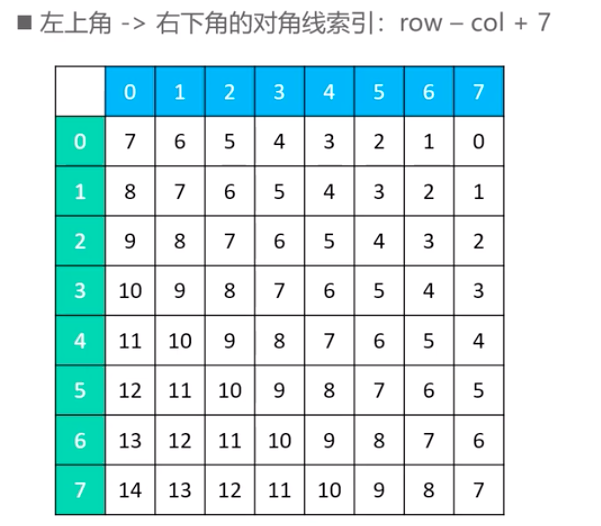
• 以八皇后为例，一共有14条从左上角到右下角的对角线。其中计算索引的方法很简单，我们只需要稍加验证，便可以得到index=row-col+7,有了这个索引，我们就非常方便了。如果该位置可以摆放皇后，直接赋值为true即可.

• 同理，一共有14条从右上角到左下角的对角线，如下图所示

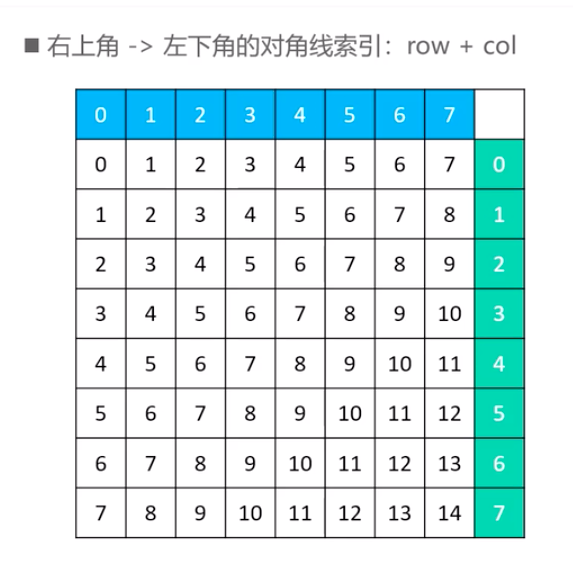
计算索引的方法同样也很简单 index=row+col.

此时，我们提交代码。但是很意外的发现，明明我们的逻辑是正确的，为什么得到的结果会有偏差呢？

• 在这里我们要明确一点，当我们的代码来到place(row+1)这一行时，即代表我们已经进入到回溯步骤。此时我们要”还原现场”。当我们发现这条路走不通时，我们应该将该条路的状态全部还原一遍，以免影响后面的操作.

/**
	  * 左上角->右下角的对角线索引 row-col+n-1
	  * 右上角->左下角的对角线索引 row+col
	  */
	 for(int col=0;col<cols.length;col++) {
		if(cols[col])  continue;
		int ltIndex=row-col+cols.length-1;
		if(leftTop[ltIndex]) continue;
		int rtIndex=row+col;
		if(rightTop[rtIndex]) continue;
		cols[col]=true;
		leftTop[ltIndex]=true;
		rightTop[rtIndex]=true;
		place(row+1);
		//回溯法需要重置boolean类型
		cols[col]=false;
		leftTop[ltIndex]=false;
		rightTop[rtIndex]=false;
	 }

即我们在来到回溯步骤时，应该将刚才的所有状态重新设置为false。

进一步的思考

• 这样就引发了一个问题，为什么我们在”八皇后问题一”中，并没有对数组进行重新赋值呢。比如我们在进入回溯步骤后，我们是否应该对数组进行重新赋值。

• 如果我们认真思考，会发现这个步骤“是多余的！”。想象一下这种情况，如果发现第5行第3列可以摆放皇后，即cols[5]=3。此时如果发现下一步走不通了，我们要回溯到上一步，如果发现第5行的第7列又可以摆放皇后，即此时cols[5]=7.数组会自动覆盖上一次的值。

• 而boolean类型的数组则不同，如果发现第5行第3列可以摆放皇后，即此时cols[3]=true，此时如果发现下一步走不通了，我们要回溯到上一步，如果发现第5行的第7列又可以摆放皇后，即此时cols[7]=true.但这显然是不合常理的，我们应该要将关于第三列的状态重新设置为false，关于对角线的状态也要设置为false。这就是两种解法的不同之处。

相信有了上面的分析，你对八皇后的理解应该又深了一步！！！

赏

谢谢你请我喝奶茶

微信