八皇后问题一

2020-04-01

回溯算法-N皇后问题

N皇后问题，是一个古老而著名的问题。我们以八皇后为例，该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。 高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。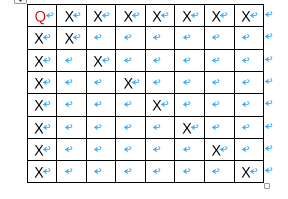

如图所示，在第一行摆放第一个皇后，打X的位置就不能够再继续摆列皇后。这时候，我们往第二行摆放皇后,如下图所示。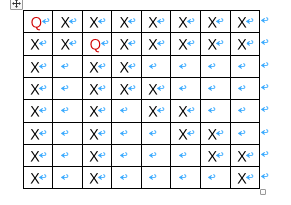

明显摆放皇后是一个递归过程,当我们继续摆放皇后，如下图所示。发现摆到第6个皇后的时候已经没有地方摆了，这时候我们可以退回到上一步，也就是所谓的回溯思想。然后继续往下摆。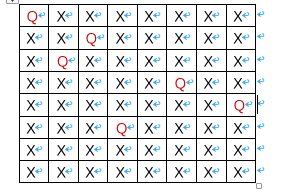
在这里插入图片描述
八皇后的一种正确摆法：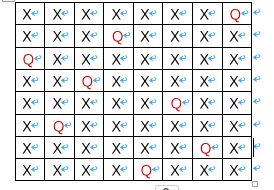

那么，我们究竟该如何实现N皇后的摆法。如何实现递归+回溯呢？

接下来我们以八皇后为例，详细探究实现方法
引入leetcode第52号问题
https://leetcode-cn.com/problems/n-queens-ii/.

我们声明一个数组，用其来存放皇后的位置。其中数组的索引为行号，数组元素为列号。For example , arr[3]=5，表明第3行的皇后在第5列。

class Solution {

       //数组索引代表行，元素代表列
    private int cols[];
    //声明一共有多少种摆法
    private int count;
    
    public int totalNQueens(int n) {
        if(n<1) return 0;
        cols=new int[n];
        place(0);
          return count;

    }

       //从第row行开始摆放皇后
    void place( int row){
    //当到达第8行时，递归结束。
        if(row==cols.length){
            count++;
            return ;
        }
        
        for(int col=0;col<cols.length;col++){
        //当第row行，第col列可以摆放时，将元素存进数组中
            if(isValid(row,col)){
            cols[row]=col;
            //摆放下一行，这时候如果不能摆放的话，会回溯到上一行
            place(row+1);
        }

        }
        

    }
    //该问题的关键，就是如何确定能不能摆放皇后
    boolean isValid(int row,int col){
        for(int i=0;i<row;i++){
            //表明第col列 已有皇后
            if(cols[i]==col) return false;
            //通过斜率的思想，表明斜线上有皇后
            if(row-i==Math.abs(col-cols[i])) return false;
        }
        return true;

    }


    
}

通过以上算法，我们得出八皇后的解法一共有92种！算是基本实现啦！
如果我们想打印出皇后的位置，由于八皇后解法太多，不容易展示，我们以四皇后为例。
以打印二维数组的思想打印摆放位置
我们只需要加入一个打印函数


 void show() {
for(int row=0;row<cols.length;row++) {
	for(int col=0;col<cols.length;col++) {
	//col[row]==col，即代表该位置可以摆放皇后
			 if(cols[row]==col) {
				 System.out.print("Q ");
			 }else {
				 System.out.print(". ");
			 }
			
		 }
		 
		 System.out.println();
		 
	 }
	 System.out.println("---------------");
	
 }

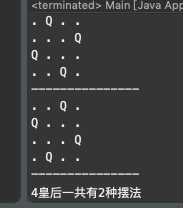
在这里插入图片描述
这时候我们通过控制台可以得到四皇后的摆放位置。

对回溯算法进行分析


/**
 * 从第row行开始摆放皇后
 * @param row
 */
 void place(int row) {
	 if(row==cols.length) {
		 count++;
		 show();
		 return;
	 }
	 for(int col=0;col<cols.length;col++) {
		 if(isValid(row, col)) {
			 //可以摆放 即在第row行，第col列摆放皇后
			 cols[row]=col;
			 place(row+1);
		 
	 }
	
	
}

以上就是我们的回溯的核心思想，其中还蕴涵了剪枝思想，我们通过判断该位置能否摆放皇后，过滤掉多余的情况。接下来打印回溯的实现过程。
很简单，我们只需要加入三行打印

 boolean isValid(int row,int col) {
		 for(int i=0;i<row;i++) {
			 //cosl[i] 即得到列号 表示第col列已经有皇后
			 if(cols[i]==col) {
System.out.println("["+row+"]["+col+"]=false");
				 return false;
				 
			 }
			
			 
			 
			// row-i==Math.abs(col-cols[i])   斜线上有皇后
			 if(row-i==Math.abs(col-cols[i])) {
System.out.println("["+row+"]["+col+"]=true");
				 return false;
			 }
				 
			 
		 }
		 
System.out.println("["+row+"]["+col+"]=true");
		 
		 
		 return  true;
	 }

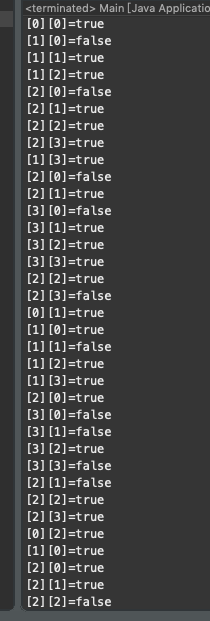
在这里插入图片描述

通过以上的分析，N皇后的解决思路已经实现。下一次，我会优化代码。提供一种新的思路！