归并排序

2020-03-29

归并排序

归并排序的思想就是不断的将当前序列平均分割成2个子序列，直到不能再分割(即此时序列中只剩下一个元素)
不断的将两个子序列进行合并，变成一个有序序列，直到最终只剩下一个有序序列

未命名文件

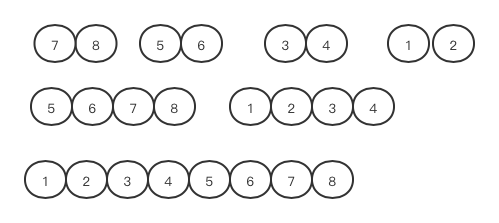
上述两个图就代表了归并排序的过程。即我们总是在归与并，当然，这其中也体现了分治和递归的思想。在后面，我会详细的介绍分治与递归！

接下来解释合并操作

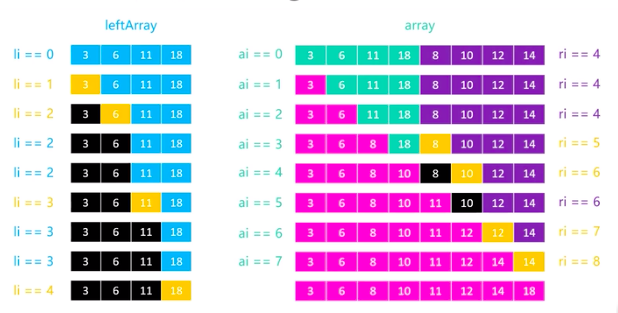
屏幕快照 2020-03-29 下午5.35.05

如上图所示，我们备份出左边数组，直接让左边数组的第一个元素即leftArray[li]与右边数组array[ri]进行比较，将小的元素存放到array[ai]位置，并且同时移动ai指针和较小元素那个数组的指针。

接下来我们考虑终止情况，如果右边先结束，即代表此时左边还没移动的元素都比右边要大，我们直接将左边的元素照搬过来即可。

如果左边先结束，此时我们什么操作都不需要进行。

代码如下所示

public class MergeSort  {
	private int leftArray[];
	private static  int arr[]= {8,7,6,5,4,3,2,1};
	/** 递归算法
	 * 对[begin,end)范围的数据进行归并排序
	 */
	private   void sort(int begin,int end) {
		
		//end-begin就是元素数量
		if(end-begin<2) return ;
		int mid=(begin+end)/2;
		sort(0,mid);
		sort(mid,end);
		merge(begin,mid,end,arr);
	}
	
	
	/**
	 * 
	 * 将[begin,mid)和(mid,end]合并起来成为一个有序序列
	 * @param begin
	 * @param mid
	 * @param end
	 */
	private   void merge(int begin,int mid,int end,int array[]) {
    //左边起始位置
		int li=0;
    //左边结束位置
		int le=mid-begin;
    //右边起始位置
		int ri=mid;
    //右边结束位置
		int re=end;
    //当前指针
		int ai=begin;
		//备份左边数组
		int leftArray[]=new int[array.length/2];
		for(int i=li;i<le;i++) {
			leftArray[i]=array[begin+i];
		}
		
		//如果左边还没有结束
		while(li<le) {
			if(ri<re && array[ri]<leftArray[li]) {
				array[ai]=array[ri];
				ri++;
				ai++;
			}else {
				array[ai]=leftArray[li];
				li++;
				ai++;	
			}	
		}
	}
	public static void main(String[] args) {
		
		MergeSort mergeSort=new MergeSort();
		mergeSort.sort(0, arr.length);
		
		for(Integer nums:arr) {
			System.out.println(nums);
		}
		
		
	}
}

下面我们来考虑归并排序的时间复杂度

T(n)=2*T(n/2)+O(n) （我们将合并操作理解为遍历左边数组和遍历右边数组，并且合并在一起，为O（n）复杂度）

T(1)=O(1)

T(n)/n=T(n/2)/(n/2)+O(1) -> 令S(n)=T(n)/n

即S(n)=S(n/2)+O(1) ->S(n)=s(n/4)+O(2) ->S(4)=S(n/8)+O(3)

一直递推，此时S(n)=S(n/2^k)+O(k)=S(1)+O(logn) 将上述代入得，S(n)=O(logn) 即此时T(n)=O(nlogn)

即我们推出归并排序的时间复杂度为O(nlogn) ，相对于我们之前所讲的冒泡排序，选择排序，插入排序，有很明显的提升！